Теплопередача

Дата добавления: 2014-05-20 | Просмотров: 1552

Теплопередача, перенос теплоты от горячего теплоносителя к холодному через разделяющую их стенку.

Теплопередача через однослойную и многослойную плоскую стенку.

Рассмотрим теплообмен между горячей жидкостью и холодной через разделяющую их плоскую однослойную стенку толщиной d с коэффициентом теплопроводности l (см. рисунок). Теплота передается от горячей жидкости к стенке конвекцией с коэффициентом теплоотдачи a₁, а от стенки к холодной жидкости – a₂.

При стационарном режиме плотность теплового потока отданного конвекцией от горячей жидкости к стенке, прошедшая через стенку за счет теплопроводности и отданная от стенки к холодной жидкости будет одинакова. Тогда процесс теплопередачи можно описать системой уравнений:

, , .

Решая эти уравнения относительно разности температур, получим:

,

или после суммирования .

Введя обозначение , окончательно можно записать ,

где k – коэффициент теплопередачи, он численно равен плотности теплового потока переданного от горячей жидкости к холодной через разделяющую их стенку при температурном напоре равном единице и характеризует интенсивность теплообмена, Вт/(м²×К).

Если стенка, разделяющая жидкости является многослойной, коэффициент теплопередачи определяется по формуле:

,

где п – количество слоев.

Теплопередача через однослойную и многослойную цилиндрическую стенку.

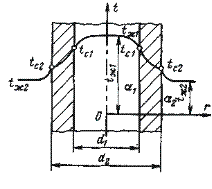Рассмотрим теплопередачу через однослойную цилиндрическую стенку, внутренний и наружный диаметр которой соответственно d₁ = 2r₁ и d₂ = 2r₂. a₁, a₂ ­– коэффициенты теплоотдачи от горячей жидкости к стенке и от стенки к холодной жидкости. Коэффициент теплопроводности материала стенки – l.

При стационарном режиме линейная плотность теплового потока отданного конвекцией от горячей жидкости к стенке, прошедшая через стенку за счет теплопроводности и отданная от стенки к холодной жидкости будет одинакова. Тогда процесс теплопередачи можно описать системой уравнений:

, , .

Решая эти уравнения относительно разности температур, получим:

,

или после суммирования .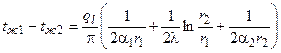

Введя обозначение , окончательно можно записать

,

где k_l – линейный коэффициент теплопередачи, он численно равен линейной плотности теплового потока переданного от горячей жидкости к холодной через разделяющую стенку при температурном напоре равном единице, Вт/(м×К).

Если стенка, разделяющая жидкости является многослойной, коэффициент теплопередачи определяется по формуле:

,

где п – количество слоев.

Критический диаметр тепловой изоляции. Тепловая изоляция применяется для уменьшения тепловых потерь в окружающую среду с поверхности теплотехнических устройств и оборудования. Для тепловой изоляции используют материалы с низким коэффициентом теплопроводности ­– асбест, шлаковая или стеклянная вата, пробка и др.

Наиболее распространен случай теплоизоляции цилиндрических поверхностей.

Рассмотрим цилиндрическую трубу (диаметры d₁, d₂), коэффициент теплопроводности l, покрытую слоем тепловой изоляции с коэффициентом теплопроводности l_из. В этом случае можно воспользоваться формулами, полученными для теплопередачи через многослойную цилиндрическую стенку записав их для двухслойной стенки. Тогда выражение для линейного термического сопротивления имеет вид

.

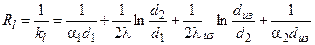Анализ выражения показывает, что при увеличении диаметра тепловой изоляции d_из термическое сопротивление теплопроводности увеличивается, а термическое сопротивление теплоотдачи 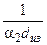уменьшается, а функция R_l = f(d_из) имеет вид представленный на рисунке. Поскольку связь между линейной плотностью теплового потока q_l и R_l обратно пропорциональная (q_l ~ R_l^-1), то q_l вначале растет, а затем уменьшается. Это приводит к тому, что при определенном значении диаметра изоляции тепловые потери изолированного трубопровода будут больше, чем неизолированного.

Диаметр изоляции, при котором теплопотери максимальны, называется критическим. Величина критического диаметра определяется из условия минимума функции R_l = f(d_из), т.е. . В результате получается выражение , где a₂ – коэффициент теплоотдачи в окружающую среду.

Для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше наружного диаметра неизолированного трубопровода. При выборе изоляции можно воспользоваться условием .

Интенсификация теплопередачи. Рассмотрим теплопередачу через плоскую однослойную стенку. Плотность теплового потока, в этом случае, равна , где R_k ­– термическое сопротивление теплопередачи .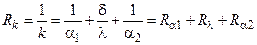

Согласно приведенным формулам, для интенсификации теплопередачи нужно либо увеличивать температурный напор, либо уменьшить термическое сопротивле­ние теплопередачи R_k. Температуры теплоносителей обусловлены требо­ваниями технологического процесса, поэтому изменить их обычно не уда­ется.

Величину термического сопротив­ления R_k можно уменьшить различ­ными способами, воздействуя на лю­бую из составляющих R_a1, R_a2, R_l. Интенсифи­цировать конвективный теплообмен и уменьшить R_aможно путем увели­чения скорости движения теплоноси­теля, турбулизации пограничного слоя и т. д. Величина термического сопротивления теплопроводности R_lзависит от материала и толщины стенки. Однако прежде чем выбирать методы воздействия на процесс теп­лопередачи, необходимо установить вклад отдельных составляющих в суммарную величину R_k. Существенное влия­ние на величину R_k будет оказывать уменьшение наибольшего из слагае­мых.

В широко используемом в тех­нике процессе передачи теплоты от капельных жидкостей к газам через металлическую стенку наибольшее термическое сопротивление имеет место в процессе теплоотдачи от га­за к стенке, а остальные сопротивления пренебрежимо малы по сравнению с ним.

В таких случаях для интенсифи­кации теплопередачи очень часто применяют оребрение той поверхности стенки, теплоотдача от которой менее интенсивна. За счет увеличе­ния площади оребренной поверхности стенки термическое сопротив­ление теплоотдачи с этой стороны стенки уменьшается, и соответственно уменьшается значе­ние R_k. Аналогичного результата можно было бы достигнуть, увели­чив коэффициент теплоотдачи, но для этого требу­ются дополнительные затраты мощ­ности на увеличение скорости тече­ния теплоносителя.