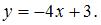|
ПРАКТИКУМ 6
Дата добавления: 2014-09-29 | Просмотров: 1716
|
|
ЗАДАНИЕ N 1
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:

Тогда этой линии принадлежат точки … 


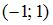
Решение:
Используя одну из координат точки, найдем значение t и, подставив его в другое уравнение, получим вторую координату точки.
 Точка с координатами
Точка с координатами  принадлежит данной линии.
принадлежит данной линии.
 Точка с координатами
Точка с координатами  принадлежит данной линии.
принадлежит данной линии.
 Точка с координатами
Точка с координатами  не принадлежит данной линии.
не принадлежит данной линии.
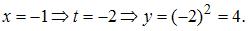 Точка с координатами
Точка с координатами 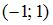 не принадлежит данной линии.
не принадлежит данной линии.
ЗАДАНИЕ N 2
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:

Тогда этой линии принадлежат точки …  ,
, 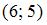 ,
,  ,
, 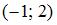
Решение:
Используя одну из координат точки, найдем значение t и, подставив его в другое уравнение, получим вторую координату точки.
 Точка с координатами
Точка с координатами  принадлежит данной линии.
принадлежит данной линии.
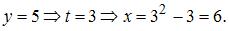 Точка с координатами
Точка с координатами 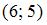 принадлежит данной линии.
принадлежит данной линии.
 Точка с координатами
Точка с координатами  не принадлежит данной линии.
не принадлежит данной линии.
 Точка с координатами
Точка с координатами 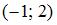 не принадлежит данной линии.
не принадлежит данной линии.
ЗАДАНИЕ N 3
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:

Тогда этой линии принадлежат точки … 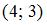 ,
,  ,
,  ,
, 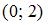
Решение:
Используя одну из координат точки, найдем значение t и, подставив его в другое уравнение, получим вторую координату точки.
 Точка с координатами
Точка с координатами 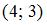 принадлежит данной линии.
принадлежит данной линии.
 Точка с координатами
Точка с координатами  принадлежит данной линии.
принадлежит данной линии.
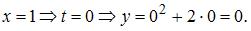 Точка с координатами
Точка с координатами  не принадлежит данной линии.
не принадлежит данной линии.
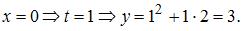 Точка с координатами
Точка с координатами 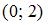 не принадлежит данной линии.
не принадлежит данной линии.
ЗАДАНИЕ N 4
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана уравнением 
Тогда эта линия проходит через точки …  ,
,  ,
,  ,
, 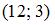
Решение:
Нужно подставить координаты данных точек в уравнение линии. Если получится тождество, то линия проходит через точку. В противном случае − нет.
1.  .
.  Точка с координатами
Точка с координатами  принадлежит линии.
принадлежит линии.
2.  .
.  Точка с координатами
Точка с координатами  принадлежит линии.
принадлежит линии.
1.  .
.  Точка с координатами
Точка с координатами  не принадлежит линии.
не принадлежит линии.
4. 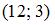 .
.  Точка с координатами
Точка с координатами 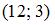 не принадлежит линии.
не принадлежит линии.
ЗАДАНИЕ N 5
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, имеет вид
 Тогда для точек
Тогда для точек  и
и  уравнение прямой может быть записано в виде …
уравнение прямой может быть записано в виде …
Решение:
Воспользуемся формулой:  Имеем:
Имеем: 
 Проделав элементарные преобразования, получим
Проделав элементарные преобразования, получим 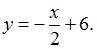
ЗАДАНИЕ N 6
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, может быть получено по формуле 
Тогда для точек  и
и  уравнением прямой является …
уравнением прямой является …
Решение:
Воспользуемся формулой 
Имеем:  или
или 
Проделав элементарные преобразования, получим 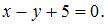
ЗАДАНИЕ N 7
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, может быть получено по формуле 
Тогда для точек  и
и  уравнением прямой является …
уравнением прямой является …
Решение:
Воспользуемся формулой 
Имеем: 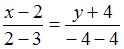 или
или 
Проделав элементарные преобразования, получим 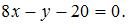
ЗАДАНИЕ N 8
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, имеет вид  тогда для точек
тогда для точек  и
и  уравнение прямой может быть записано в виде …
уравнение прямой может быть записано в виде …
Решение:
Воспользуемся формулой:  Имеем:
Имеем: 
 Проделав элементарные преобразования, получим
Проделав элементарные преобразования, получим