Выбор схемы регулирования водораспределения

Дата добавления: 2014-05-29 | Просмотров: 1533

<== предыдущая страница | Следующая страница ==>

 

При проектировании автоматизации водораспределения на оросительной системе выбор схемы регулирования производится с учётом данных по уклонам, по расходам, по типу дождевальных машин, а также с учётом стадии автоматизации и назначения каналов оросительной системы.

Для заданных условий работы межхозяйственной сети, при новом проектировании с поливом дождевальными машинами при средних уклонах поверхности земли по трассе канала принимается схема регулирования II класса в виде каскадного регулирования с перетекающими объёмами.

Для выбранной схемы регулирования характерны следующие особенности:

- водораспределение осуществляется по запросам потребителей, в пределах плана водопользования, снизу вверх;

- наличие свободных статических напоров или обратной связи между бьефами;

- создание необходимых объёмов регулирования;

- пропорциональное соответствие поступающих в бьеф расходов и расходов потребителей;

- стабилизация уровней в средней части бьефа;

- импульсно – паузный закон перерегулирования перегораживающих сооружений;

- учёт волновых процессов;

- минимизация непроизводственных сбросов из канала.

 

Расчёт оптимальной длины бьефа

Основной фактор качества и эффективности схемы регулирования водораспределения и оросительной системы в целом — это оптимальное количество сооружений при оптимальных длинах бьефов.

Длина бьефа не должна быть меньше минимальной необходимой длины, определяемой по времени добегания волны, вызванной включением водопотребителей в конце бьефа, до регулятора и времени подачи в бьеф необходимого расхода воды.

Минимальная необходимая длина бьефа, обеспечивающая процесс перерегулирования при каскадном регулировании определяются из уравнения или по номограммам:

где l - искомое значение длины бьефа, м; m- заложение откосов канала; I - уклон дна канала; b – ширина канала по дну, м; h - нормальная бытовая глубина воды в канале, м; V - скорость воды при h , м/с; t - время открытия регулятора, сек; k – коэффициент, зависящий от глубины и глубины канала, k=1.1÷1.5; - расход мгновенно включающихся потребителей, м3/с.

Длина бьефа должна учитывать соотношения капиталовложений на устройство горизонтальных дополнительных дамб при более длинных каналах и капиталовложений на устройство дополнительных перегораживающих сооружений. В этом случае оптимальная по капиталовложениям длина бьефа определяется по зависимости или по номограммам:

Для каналов в полувыемке-полунасыпи в облицованном русле:

*Sз*m,*I2д*lopt3+[Sз*(bдам+2*m,*Hн)+2*S0* ]*Iд*lopt2-Sc=0

где lopt- искомая длина бьефа, м;Hн- средняя высота насыпи, м; bдам -ширина дамбы по верху, м;m- заложение откосов канала;m,- ½*(mн+m), где mн- заложения наружных откосов дамб, при mн=m получаем m,=m;Iд- уклон дна канала;Sз- стоимость 1м3 насыпи, грн.;Sо- стоимость 1м2 облицовки, грн.;Sс- стоимость перегораживающих сооружений, грн.

По номограмме lmin=800 м, а lopt=1000 м.

Так как lmin=800 м <lopt=1000 м, к дальнейшему расчёту принимаем lopt=1000 м.

 

Принципы расчёта переходных процессов в каналах оросительных систем с автоматическим регулированием водоподачи

Характерной особенностью работы каналов каскадного регулирования является динамичность происходящих в них процессов, обусловленная изменениями как во времени, так и по длине русла.

Такие процессы, возникающие в период перерегулирования водопотребления (перехода от одного установившегося режима к другому), а также при различных аварийных ситуациях, называют переходными. Основной переходных процессов является неустановившееся движение воды в оросительном канале.

При регулировании с перетекающими объёмами основным принципом схемы является постоянство уровня воды в контрольном створе, расположенном в серединой части участка канала, при котором обеспечивается равенство (баланс) притока и оттока воды и, соответственно, равенство объёмов воды выше и ниже контрольного створа.

Это равенство достигается поддержанием автоматическими регуляторами перегораживающих сооружений в любой момент времени изменений уровней и самих уровней воды в начале и конце бьефа, а также в промежуточных створах, мест отбора воды сосредоточенными потребителями с помощью верхних (max) и нижних (min) уставок датчиков с заданными расчетными пределами и заданной погрешностью уровней.

Задачей расчёта переходных процессов при авторегулировании подачи воды является установление такого закона (графика или гидрографа) водоподачи на перегораживающих сооружениях при известных (заданных) условиях водопотребления, который бы обеспечивал оптимальные переходные процессы на магистральном канале. Под критерием оптимальности в этом случае принимается следующее: переходный процесс от одного режима к другому режиму должен происходить достаточно быстро при минимальных колебаниях уровней и расходов воды в канале с последующим их затуханием.

Математической моделью переходных процессов является краевая задача для уравнений Сен-Венана, которую целесообразно решать одним из численных методов. Уравнение Сен-Винана для рассматриваемой задачи удобно представить в таком виде: , гдеy=(i0+wl)*Fr –(Q /K2),

где Z –отметка уровня; V – средняя в сечении скорость V= 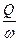; с- скорость распространения малых возмущений c= ; q – боковой сток, приходящийся на единицу длины русла; F - число Фруда F =V2/C2; - частная производная , учитывающая непризматичность русла; В- ширина потока по верху; i0- уклон дна канала; К- расходная характеристика 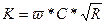, С- коэффициент Шези (скоростной множитель).

Искомыми функциями в системе является z=z(l;t) и Q=Q(l;t).

Начальное условие – состояние покоя с горизонтальной поверхностью воды или установившийся режим движения. Для равномерного движения h(l;0)=const илиz(h+i0*l;0)=const и Q(l;0)=const. Для неравномерного установившегося движения функция Z(l;0) определяется с помощью построения кривых свободной поверхности при Q(l;0)=const.

Левое граничное условие- функция уровня или открытие затвора от времени и уровня воды в контрольном створе : z=z(t;zконтр) или a=a(t; zконтр).

 

Построение кривой свободной поверхности по методу Б. А. Бахметева.

 

 

Для призматических русел с прямым уклоном дна допускается в предварительных расчётах считать движение жидкости неравномерным установившемся. Тогда решения дифференциальных уравнений движения сводятся к определению глубин воды в определенных створах. С учётом принятия постоянными и равными их среднему значению между двумя сечениями величин гидравлического показателя русла (x) и характеристики изменения удельной кинетической энергии вдоль потока (j), определение кривой свободной поверхности воды выполняется с использованием функций Б. А. Бахметева:

,

где iд- уклон дна канала; l- длина бьефа (расстояние между створами),м; h0- нормальная бытовая глубина (глубина воды в нормальном створе),м; - относительные глубины воды при hн- глубина в начале бьефа, м; hк- глубина в конце бьефа, м; 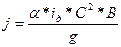- характеристика изменения удельной кинетической энергии вдоль потока:

- коэффициент Кариолиса ;

С- коэффициент Шези (скоростной множитель);

g- ускорение свободного падения;

В- ширина по верху при бытовой глубине.

- функция Б. А. Бахметева,

где х- гидравлический показатель русла

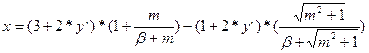
(или )

Расчёт выполняется в следующей последовательности:

- определяется нормальная бытовая глубина h0 и глубина в конце бьефа при стабилизации уровня hk;

- определяется относительная глубина ;

- находится значение функции Бахметева Ф( ) для определенного значения x;

- рассчитывается значение характеристики изменения кинетической энергии потока j и значения (1-j);

- определяется отношение ;

- подбирается сочетание и Ф ( ) для определённого значения х;

- определяют глубину воды h=hн= .

Расчёт ведут пошагово по расчётным сечениям считая х и постоянными в пределах бьефа, а - переменной.

Результаты вычислений представляют в табличной форме и в виде графика кривой свободных поверхностей воды в бьефе по длине бьефа.

 


1 | 2 | 3 | 4 |

При использовании материала ссылка на сайт Конспекта.Нет обязательна! (0.048 сек.)