Расчет контурной площади контакта и контурного давления

Дата добавления: 2014-06-18 | Просмотров: 1637

давления Для небольших поверхностей, когда волнистость не обнаруживается

А =А .

с а

Для больших поверхностей для расчета А_с используется модель волн в виде сферических сегментов.

Если шероховатость поверхности невелика (R_mах < 0,1H_B ) то для расчета можно использовать

зависимости, основанные на формулах Герца. В этом случае:

а) если число контактирующих волн n_в < 3, т.е. в случае малых нагрузок и малых номинальных

площадей (А_а ~ S_В):

A_c=

p_c=

Где S_B— шаг волны;

R_B — приведенный радиус волн, б) если n_в > 3 , т.е. при А_а » S_B²

A_c=2.2*A^0.14*(R_B/H_B)^0.43 *(θ*N)^0.86

р_a =0,45*( H_b/R_b*θ²)^0.43*p_a^0.14

При использовании аналогичного подхода получены формулы для расчета:

сближения поверхностей;

объем межконтактного пространства и среднего зазора;

числа пятен контакта, их средней площади и размера среднего расстояния

между ними.

4.3. Расчет на износ узлов трения без смазочного материала и при граничной смазке (Расчет на

износостойкость)

При проведении расчетов на износ в основном реализуются три подхода:

1 - получение расчетных зависимостей на основе анализа процессов на

микроуровне - фактической площади контакта.

2 - использование закона изнашивания

I= k*р^т *υⁿ,

где k, m, n - определяются экспериментально. Однако для многих практически важных случаев m=1, n=0, поэтому

I=k*р.

3 - использование эмпирических уравнений износа для конкретных узлов

трения, полученных при натурных или модельных испытаниях.

Первый подход реализован И.В. Крагельским в рамках предложенной им в 1939 году усталостной теории изнашивания.

Основы усталостной теории изнашивания.

Вследствие шероховатости реальных тел их взаимодействие при трении является дискретным, касание происходит на отдельных участках, под действием нормальной нагрузки взаимно внедряются или расплющиваются, а в области пятен фактического контакта возникают соответствующие напряжения и деформации. При трении приповерхностные слои испытывают многократно повторяющиеся воздействия: перед выступом скользящей микронеровности существует зона сжатия, а за ним - зона растяжения. В результате возникает знакопеременный цикл нагружения материала, что и вызывает его усталостное разрушение.

Задача о расчете износа делится на две части:

- вычисление объема материала, который интенсивно деформируется при
трении;

- выявление условий разрушения этого объема.

При расчете, с учетом того, что материал удаляется лишь с фактических пятен касания, вводится понятие удельной интенсивности изнашивания:

i=V_g /A_r*d

где V_g - объем материала, удаленного с площади А_r (ФПК) при пути трения равном диаметру пятна контакта.

Между величинами I (интенсивность изнашивания) и i (удельная интенсивность изнашивания) существует связь:

I=i*(A_r/A_a)

ИЛИ

I=i*(p_a/p_r).

Рассмотрим контактирование абсолютно твердого шероховатого тела, перемещающегося по гладкой поверхности упругодеформируемого изнашиваемого контртела (например, пара трения металл-полимер).

В этом случае, моделируя шероховатость как и при расчете ФПК набором сферических сегментов, имеем:

i=h/3d_n

где h - глубина внедрения,

n - число циклов, приводящих к разрушению (отделению объема V_g),

n=1...10⁵.

Число n зависит от напряженного состояния единичного пятна контакта и характера физико-механических процессов.

Из геометрических соображений для упругого контакта сферы и деформируемой плоскости:

где г - радиус вершины микронеровности Окончательно:

Величина п находится по кривой усталости при известных действующих переменных напряжениях, описываемой уравнением:

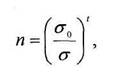
где σ₀ и t - экспериментальные константы (t= 1,3... 1,4), зависящие от материалов пары трения и смазочного материала.

где к=3 для высокоэластичных материалов,

f - коэффициент трения. В результате получена формула:

в которой R_max - максимальная высота микронеровностей.

В рамках усталостной теории изнашивания получены формулы, по которым может быть вычислена интенсивность изнашивания при пластическом контакте неровностей, а также в случае двух шероховатых тел и т.п.

К сожалению, приведенная теория в недостаточной степени учитывает сложные многообразные процессы, происходящие при трении и изнашивании, и поэтому пока имеет довольно ограниченное применение.