АНАЛИЗ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ВЕТВЕЙ

Дата добавления: 2014-05-29 | Просмотров: 1688

Во многих случаях приходится встречаться с расчетом сложных электрических цепей синусоидального тока, которые в общем случае являются цепями со смешанным соединением сопротивлений (рисунок 3.1). Эти электрические цепи могут быть разделены на участки с последовательным и участки с параллельным соединением сопротивлений.

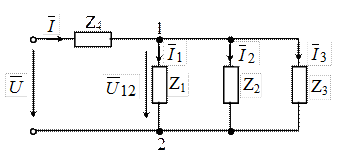
Рисунок 3.1. Смешанное соединение сопротивлений электрической цепи

При параллельном соединении сопротивлений параллельные ветви электрической цепи находятся под одним и тем же напряжением U = U₁₂, поэтому для каждой из этих ветвей определение всех расчетных величин производится по формулам, справедливым для отдельных сопротивлений электрических цепей с последовательным соединением сопротивлений. Для участка цепи с параллельным соединением сопротивлений ток на разветвленном участке определяется в соответствии с первым законом Кирхгофа, записанным для узла разветвления в векторной форме:

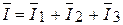. (3.1)

Этот ток можно определить графически с помощью векторной диаграммы, как сумму составляющих векторов токов.

Токи в отдельных ветвях электрической цепи могут быть определены через проводимости (y) соответствующих ветвей:

I₁ = U₁₂×y₁; I₂ = U₁₂×y₂; I₃ = U₁₂×y₃. (3.2)

При этом ток в неразветвленной части цепи равен произведению напряжения U₁₂ на параллельном участке цепи на сумму проводимостей параллельно включенных сопротивлений

I = U₁₂×(y₁ + y₂ + y₃). (3.3)

Сопротивления отдельных ветвей могут носить активно-реактивный характер при наличии индуктивных Х_L и емкостных Х_C сопротивлений, поэтому в общем случае сопротивления могут быть определены через активные g и реактивные b проводимости:

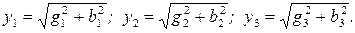(3.4)

При этом активные и реактивные проводимости:

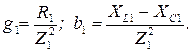(3.5)

При параллельном соединении индуктивного и емкостного сопротивлений (рисунок 3.2, а) в электрической цепи возможен резонанс токов (особое состояние электрической цепи при параллельном соединении катушки индуктивности L и конденсатора C, при которых реактивная индуктивная проводимость равна реактивной емкостной проводимости, т.е. b_L = b_C).

Полная проводимость электрической цепи y при резонансе токов оказывается минимальной, равной активной проводимости цепи .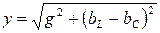

Векторная диаграмма токов и напряжений при резонансе токов приведена на рисунке 3.2 б. Коэффициент мощности в электрической цепи cosj = g/y = 1 принимает максимальное значение, а угол сдвига фаз между током и напряжением j = 0, поэтому при резонансе токов напряжение U и общий ток I совпадают по фазе. При смешанном соединении сопротивлений (рисунок 3.1) электрическая цепь при расчете приводится к виду (рисунок 3.3). Полное сопротивление Z₁₂ участка цепи 1-2 может быть определено через ее проводимость Z₁₂ = 1/y₁₂. При этом расчет электрической цепи со смешанным соединением сопротивлений сводится к расчету простейшей электрической цепи с последовательным соединением сопротивлений.

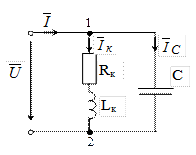а	б
Рисунок 3.2. Электрическая цепь с параллельным соединением катушки индуктивности и конденсатора: а – электрическая схема; б – векторная диаграмма

Рисунок 3.3. Электрическая цепь после преобразования

При параллельном и смешанном соединении сопротивлений векторную диаграмму строят, начиная с вектора напряжения U₁₂ на параллельном участке цепи.