Гидростатика

Дата добавления: 2014-07-19 | Просмотров: 1622

3.1. Основное уравнение гидростатики

На практике часто приходится иметь дело с жидкостью, находящейся в состоянии покоя, т.е. когда отсутствуют перемещения отдельных ее частиц относительно друг друга.

Покоящаяся жидкость может быть подвержена действиям внешних сил, которые делятся на силы массовые и силы поверхностные.

Массовые силы пропорциональны массе жидкости. К ним относятся силы тяжести и силы инерции.

Поверхностные силы действуют на поверхность рассматриваемых объемов жидкостей, например сила атмосферного давления, сила давления газа или пара, сила давления поршня.

В результате действия внешних сил внутри покоящейся жидкости возникает напряжение, называемое гидростатическим давлением.

В состоянии покоя жидкость обладает потенциальной энергией, состоящей из потенциальной энергии давления и потенциальной энергии положения.

Общее выражение потенциальной энергии давления можно получить, определив давление поршня р_S на некоторый объем жидкости V (рис. 3.1).

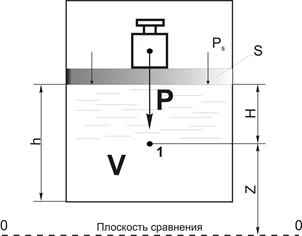
Рис. 3.1. К определению потенциальной энергии жидкости

Под действием груза Р жидкость находится под давлением

р_S = р/ S,

где S – площадь поршня.

Потенциальная энергия давления Е_п.д равна потенциальной энергии груза, равного рh. Заменив р через рS и учитывая, что

Sh=V, а V=m/ρ,

получим, что потенциальная энергия давления равна произведению давления на объем

Е_п.д =рh = р_s Sh =р_SV = p_S m/ρ. (3.1)

Потенциальная энергия положения определяется высотой Z центра тяжести объема жидкости над некоторой произвольно выбранной горизонтальной плоскостью, называемой плоскостью сравнения (например, поверхность земли, пола и т.п.)

Потенциальная энергия положения равна произведению веса жидкости G в объеме V на высоту положения Z, которую называют также нивелирной высотой или геометрическим напором. С учетом того, что масса жидкости

(m=G/g),

получим

Е_п.пол= GZ=mgZ. (3.2)

Общая потенциальная энергия жидкости

Е_п.= Е_п.д.+ Е_п.пол.= ( р_Sm/r ) + mgZ. (3.3.)

Разделив левые и правые части уравнения (3.3) на единицу веса mg, получим удельную потенциальную энергию жидкости

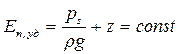( 3.4)

Величину (p_s/ρg) называют гидростатическим или пьезометрическим напором.

Уравнение (3.4) называют уравнением гидростатики. Найдем (рис. 3.1) значение const (с): при (Z+H) давление на поверхности жидкости под поршнем равно р_s, тогда

.

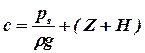Константа с выражает запас потенциальной энергии единицы веса жидкости, находящейся под давлением p_s и поднятой на высоту (Z+H), относительно выбранной плоскости сравнения.

Найдем значение давления в точке 1:

,

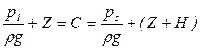откуда

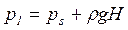. (3.5)

Давление в любой точке жидкости зависит от величины давления р_s и глубины ее погружения H. При увеличении глубины погружения H пьезометрический напор уменьшается, а их сумма остается неизменной.

Разделив левые и правые части уравнения (3.3) на единицу веса в Н, получаем размерность, выраженную высотой столба данной жидкости в метрах:

.

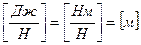Это означает, что единица веса жидкости р в 1 Н, имеющая массу 0,102 кг (m = р/g = 1/9,8 = 0,102 кг) и поднятая на 1 м, обладает потенциальной энергией положения в 1Дж, если на 30 м, то – в 30 Дж .

Согласно основному уравнению гидростатики, сумма удельных потенциальных энергий положения и давления в покоящейся жидкости есть величина постоянная и равная полному гидростатическому напору.

Из уравнения гидростатики следует закон Паскаля (1650 г.): давление, создаваемое в любой точке внутри одного и того же объема несжимаемой жидкости, находящейся в покое, передается одинаково всем точкам этого объема ( формула 3.5).

Из уравнения (3.4) следует, что энергию жидкости можно изменять следующими способами:

увеличением высоты положения жидкости, например высотой плотины ГЭС, увеличением высоты водонапорной башни;

путем создания давления, например насосами, компрессорными машинами.