Реологічні моделі тіл.

Дата добавления: 2014-10-03 | Просмотров: 1837

Структурно-механічні властивості називають також реологічними властивостями.

Реологія – це наука, яка вивчає механічні властивості тіл через деформації під дією зовнішніх напруг. Деформацією (e) називають відносне зміщення точок системи, при якому не порушується її цілісність. Напруження (Р) – це відношення сили яка викликає деформацію до площі на яку вона діє.

В реології механічні властивості матеріалів представляють у вигляді реологічних моделей. В їх основі лежать три основні закони, що пов’язують напруження з деформацією.

Модель ідеально пружного тіла Гука. Деформація пружного тіла прямо пропорційна напруженню зсуву:

e = P/E ( 8.43)

P - напруження зсуву.

E - Модуль Юнга.

Закон моделюється ідеальною пружиною.

Рис. 66. Модель ідеально пружного тіла.

Залежність деформація від часу та від напруження для ідеально пружного тіла наведено на рис.67.

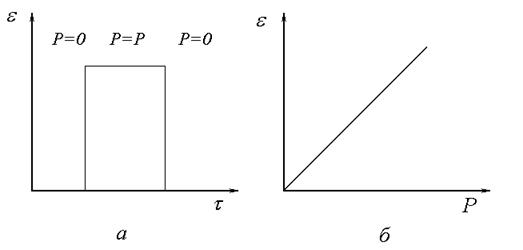
Рис. 67. Залежність деформації від часу (а) напруження (б) для ідеальної пружини.

Модель ідеально в’язкого тіла Ньютона. Моделюється поршнем, що вільно рухається у нескінченно довгому циліндрі заповненому в’язкою рідиною. Для ідеально - в’язкого тіла характерна здатність до течії, тобто деформації під дією як завгодно малого навантаження на протязі нескінченно великого часу.

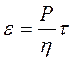
( 8.44)

Швидкість деформації цього тіла прямо пропорційна напруженню зсуву.

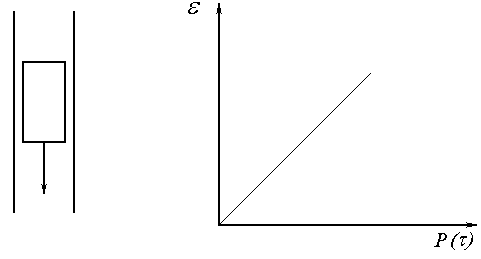
Рис. 68. Модель ідеально в’язкого тіла.

Модель ідеального пластичного тіла Сен-Венана – Кулона. Моделюється твердим тілом, що знаходиться на рівній поверхні. Деформація в системі відсутня, якщо напруження зсуву менше якогось значення Р_Т, яке називається межею текучості.

P< Р_Т e=0 ( 8.45)

При досягненні цього значення деформація не має межі і відбувається з будь якою швидкістю.

P= Р_Т e>0 ( 8.46)

Рис. 69. Модель ідеального пластичного тіла.

Складні моделі складаються з декількох ідеальних сполучених паралельно, чи послідовно. При послідовному з’єднанні елементів повне навантаження припадає на кожен елемент, а повна деформація та її швидкість складається з деформацій та швидкостей з’єднаних елементів:

P= Р₁ = Р₂= ... = Р_n

; ( 8.47)

При паралельному з’єднані елементів деформація та її швидкість однакові для всіх елементів, а повне навантаження складається з навантажень окремих елементів:

P= Р₁ + Р₂+ ... + Р_n

; ( 8.48)

В моделі Максвела послідовно з’єднанні елементи Гука і Ньютона. При послідовному з’єднанні загальне навантаження повністю передається на обидва елемента. Загальна деформація та її швидкість складаються з параметрів окремих елементів:

( 8.49)

Рис. 70. Модель пружно – в’язкого тіла Максвела (а), залежності його деформації (б) та напруження(в) від часу.

При миттєвій фіксованій деформації відбувається миттєве розтягнення моделі зі збереженням в подальшому постійної деформації (e = const). Після цього внутрішнє напруження поступово спадає (відбувається релаксація) внаслідок деформації в’язкого елемента. За цих умов швидкість деформації рівна нулю і рівняння (8.48) має вигляд:

( 8.50)

( 8.51)

Інтегруванням цього виразу в межах від Р_о до Р одержуємо:

( 8.52)

( 8.53)

де l=h/E – час релаксації напруження.

Величина l це час за який початкове напруження в тілі зменшиться в е раз. Чим більше значення часу релаксації тим повільніше відбувається релаксація. Модель Максвела являє собою пружно-в’язку рідину, що здатна до течії при дії будь-якого навантаження. Для цієї моделі характерна необерненість деформації. Ця модель показує, що відмінності між рідинами та твердими тілами мають лише кінетичний характер. Якщо час релаксації значно більший за час дії напруження то таке тіло є твердим, якщо час релаксації менший за час дії напруження тіло поводить себе як рідина – напруження зменшуються завдяки течії.

Модель Кельвіна – Фойгта являє собою в’язко – пружне тіло, що здатне відновлювати свої властивості після зняття напруження. Ця модель складається з паралельно з’єднаних елементів Гука і Ньютона. Для цієї моделі:

( 8.54)

( 8.55)

деформація в такому тілі під дією постійного навантаження Р₀ зростає. Швидкість деформації з часом зменшується, тому що на пружній елемент припадає все більше зусилля. Коли швидкість деформації стає рівною нулю деформація досягає максимального значення. За умови постійного навантаження модель Кельвіна – Фойгта описується рівнянням:

( 8.56)

Розв’язком цього рівняння є :

( 8.57)

Рис. 71. Модель в’язко – пружного тіла Кельвіна – Фойгта (а) та залежність деформації від часу (б).

Якщо зняти навантаження після досягнення певної деформації, то система вертається у вихідний стан також на протязі певного часу. При цьому рівняння (8.55) має розв’язок:

( 8.58)

де q=h/Е – час релаксації деформації.

На відміну від пружності, яка характеризується миттєвими деформаціями еластичність проявляється в часі. Чим більший час релаксації деформації, тим більша еластичність тіла.

Комбінацією трьох ідеальних елементів можна створити модель, що має структурно-механічні властивості практично будь-якого реального тіла.

Контрольні питання

1. Яка природа броунівського руху дисперсних частинок? Якою величиною характеризується інтенсивність броунівського руху?

2. B чим полягає явище дифузії? Напишіть рівняння Фіка.

3. Напишіть рівняння Ейнштейна для коефіцієнта дифузії. Проаналізуйте його.

4. Який зв’язок між середнім зсувом частинки і коефіцієнтом дифузії? Наведіть рівняння Ейнштейна – Смолуховського.

5. Що таке кінетична стійкість колоїдних систем? У чому полягає явище седиментації?

6. Напишіть формулу гіпсометричного закону. Який зв’язок між гіпсометричною висотою і кінетичною стійкістю?

7. Напишіть рівняння седиментації для сферичних частинок у полі земного тяжіння. Від яких властивостей середовища залежить константа цього рівняння?

8. Що таке монодисперсна суспензія? Полідисперсна? Накресліть графік осідання частинок монодисперсної, бідисперсної та полідисперсної системи.

9. Накресліть інтегральну і диференціальну криві седиментації для полідисперсної системи.

10. Для яких дисперсних систем застосовують седиментацію у відцентровому полі? Як у цьому випадку розрахувати радіус сферичної частинки?

11. Якими оптичними властивостями володіє колоїдна система? Що таке оптична густина?

12. У чому полягає явище світлорозсіювання? Діаграма Мі.

13. Напишіть рівняння Релея. Проаналізуйте його.

14. У чому полягає явище світлопоглинання (адсорбція світла)? Напишіть рівняння Бугера-Ламберта-Бера. Проаналізуйте його.

15. Які оптичні прилади засновані на явищі світлопоглинання?

16. Які оптичні методи визначення концентрації і дисперсності золів засновані на явищі світлорозсіювання?

17. Який принцип покладений в основу дії ультрамікроскопу? Як визначити середній радіус частинок золю за допомогою ультрамікроскопу?

18. Який принцип покладено в основу електронного мікроскопа?

19. Як визначити середній радіус частинок і концентрацію дисперсної системи за допомогою нефелометра?

20. Які властивості дисперсних систем вивчає реологія. Охарактеризуйте типи контактів між частинками.

21. Охарактеризуйте коагуляційні колоїдні структури..Що таке тиксотропія?

22. Охарактеризуйте конденсаційно кристалізаційні колоїдні структури. Приведіть приклади.

23. Напишіть рівняння Ейнштейна для в’язкості дисперсних систем. Вкажіть границі його застосування.

24. Які рідини називають неньютонівськими? Як їх класифікують.

25. Напишіть рівняння Освальда – Вейля для течії рідин. Як деформація рідин залежить від прикладеної напруги?

26. Напишіть рівняння Бінгама для твердо подібних систем. Які системи підкоряються йому? Що така гранична напруга на зрушення по Бінгаму?

27. Накресліть реологічні криві в координатах деформація - напруга для рідиноподібних та твердо подібних систем. Відзначте на графіку Р_т максимальну границю текучості.

28. Закон Гука. Модель ідеально – пружного тіла.

29. Закон Ньютона, модель ідеального пластинчатого тіла.

30. Закон Сен-Венана-Кулона. Модель ідеального пластинчатого тіла.

31. Складні реологічні моделі колоїдних систем. Модель Максвела.

32. Складні реологічні моделі колоїдних систем. Модель Кельвіна - Фойгта.